Gabbar Gunshots Probability Analysis
Everyone must have watched movie Sholay(1975). Do you remember the entry scene of Gabbar Singh (Amzad Khan)?
"Kitne Aadmi The"
Exactly That was the scene. In this scene Gabbar kills three of his henchmen. Lets skip the middle conversation and jump to this part.
Gabbar drags a revolver from one of his man and asks the number of bullets in it.
He replies "six". Generally a revolver has 6 bullets compact in a round structure.
Here the game begins.
He already made up his mind to kill all three men because he doesn't like coward people but he does not want to shoot them just like that. He wants some entertainment here.
This is the game of probability. He fires three bullets in the air to make remaining count three because he needs to kill only three people and one bullet is enough for each.
Now he revolves the cylinder of revolver in a speedy way so even he doesn't know where are the remaining three bullets.
Then he takes a shot towards each man. 3 chambers are with bullets and 3 are empty, he thinks there are 50-50 chances here.
Now lets analyze the situation here.
What we know
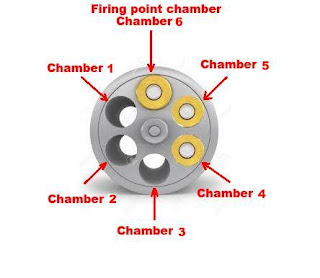
Three bullets are in a consecutive order and three empty chambers are also in consecutive order but it is a circle so any chamber can be its firing position. Only we can say confidently that there is no single empty chamber between two bullets. There is only one gap between two bullets and it is of three empty chambers.
Lets give names to each chamber. Suppose Chamber 1, Chamber 2 and Chamber 3 are empty chambers and Chamber 4, Chamber 5 and Chamber 6 are with bullets. We gave these names anti clock-wise because cylinder moves in clock wise direction so 2 will be fired after first and third will be fired after second and so on.
First shot can be empty or it can be with bullet. Nobody knows. Suppose if first shot is empty. It means either Chamber 1 or Chamber 2 or Chamber 3 in its firing position.
Suppose Chamber 1 is in its firing position during first shot then other two men will be saved because next number is of 2 and then 3 and both are empty chambers so all are saved (That's what happens in the movie)
Suppose Chamber 2 is in its firing position during first shot then second man will be saved because 3 is an empty chamber but 4 is filled with bullet it means last man (Kalia) will be killed. Even he ate salt of his master but no mercy would be here in first place.
Suppose Chamber 3 is in its firing position during first shot then second and third both men will be killed because 4 and 5 the chambers are with bullets.
Suppose Chamber 4 is in its firing position during first shot then all three will be killed because 4, 5 and 6 are with bullets.
Suppose Chamber 5 is in firing position during first shot then second will be killed and third man will be saved because 1 is empty.
Suppose Chamber 6 is in firing position during first shot then first and second both will be saved because 1 and 2 both are empty.
In this analysis, there are chances, each man can be killed and each can be saved. But can you predict what may happen with next?
You can't predict the future of first two men in any condition. You can predict the future of only last man and that's in two conditions only.
1) If First man is killed and second is saved
2) If first man is saved and second is killed
In first situation, you can easily find that chamber 6 was in firing position during first shot that's why first is killed and second is saved because second got chamber 1 which is empty. Now third man will get chamber 2 which is also empty and he will be saved too. There is no other condition for this situation.
In second situation, still you can find that chamber 3 was in firing position that's why first is saved and second is killed because second got chamber 4 which is with bullet. Now third man will get chamber 5 which is also with bullet and he will be killed too. There is no other condition for this situation too.
Both are unique situations.
Except these two conditions you can't predict future of third man.
Suppose first two are saved then you can't predict the fate of third.
He can be killed if chamber 2 was in firing position during first shot.
He can be saved if chamber 1 was in firing position during first shot.
Suppose first two are killed even then you can't predict the fate of third.
He can be killed too if chamber 4 was in firing position during first shot.
He can be saved if chamber 5 was in firing position during first shot.
Conclusion :
If second shot is different than first shot only then you can predict the behaviour of third shot.
Moral :
But after all none of this matters because eventually Gabbar would kill all three.
Everyone must have watched movie Sholay(1975). Do you remember the entry scene of Gabbar Singh (Amzad Khan)?
"Kitne Aadmi The"
Exactly That was the scene. In this scene Gabbar kills three of his henchmen. Lets skip the middle conversation and jump to this part.
Gabbar drags a revolver from one of his man and asks the number of bullets in it.
He replies "six". Generally a revolver has 6 bullets compact in a round structure.
Here the game begins.
He already made up his mind to kill all three men because he doesn't like coward people but he does not want to shoot them just like that. He wants some entertainment here.
This is the game of probability. He fires three bullets in the air to make remaining count three because he needs to kill only three people and one bullet is enough for each.
Now he revolves the cylinder of revolver in a speedy way so even he doesn't know where are the remaining three bullets.
Then he takes a shot towards each man. 3 chambers are with bullets and 3 are empty, he thinks there are 50-50 chances here.
Now lets analyze the situation here.
What we know
Three bullets are in a consecutive order and three empty chambers are also in consecutive order but it is a circle so any chamber can be its firing position. Only we can say confidently that there is no single empty chamber between two bullets. There is only one gap between two bullets and it is of three empty chambers.
Lets give names to each chamber. Suppose Chamber 1, Chamber 2 and Chamber 3 are empty chambers and Chamber 4, Chamber 5 and Chamber 6 are with bullets. We gave these names anti clock-wise because cylinder moves in clock wise direction so 2 will be fired after first and third will be fired after second and so on.
First shot can be empty or it can be with bullet. Nobody knows. Suppose if first shot is empty. It means either Chamber 1 or Chamber 2 or Chamber 3 in its firing position.
Suppose Chamber 1 is in its firing position during first shot then other two men will be saved because next number is of 2 and then 3 and both are empty chambers so all are saved (That's what happens in the movie)
Suppose Chamber 2 is in its firing position during first shot then second man will be saved because 3 is an empty chamber but 4 is filled with bullet it means last man (Kalia) will be killed. Even he ate salt of his master but no mercy would be here in first place.
Suppose Chamber 3 is in its firing position during first shot then second and third both men will be killed because 4 and 5 the chambers are with bullets.
Suppose Chamber 4 is in its firing position during first shot then all three will be killed because 4, 5 and 6 are with bullets.
Suppose Chamber 5 is in firing position during first shot then second will be killed and third man will be saved because 1 is empty.
Suppose Chamber 6 is in firing position during first shot then first and second both will be saved because 1 and 2 both are empty.
In this analysis, there are chances, each man can be killed and each can be saved. But can you predict what may happen with next?
You can't predict the future of first two men in any condition. You can predict the future of only last man and that's in two conditions only.
1) If First man is killed and second is saved
2) If first man is saved and second is killed
In first situation, you can easily find that chamber 6 was in firing position during first shot that's why first is killed and second is saved because second got chamber 1 which is empty. Now third man will get chamber 2 which is also empty and he will be saved too. There is no other condition for this situation.
In second situation, still you can find that chamber 3 was in firing position that's why first is saved and second is killed because second got chamber 4 which is with bullet. Now third man will get chamber 5 which is also with bullet and he will be killed too. There is no other condition for this situation too.
Both are unique situations.
Except these two conditions you can't predict future of third man.
Suppose first two are saved then you can't predict the fate of third.
He can be killed if chamber 2 was in firing position during first shot.
He can be saved if chamber 1 was in firing position during first shot.
Suppose first two are killed even then you can't predict the fate of third.
He can be killed too if chamber 4 was in firing position during first shot.
He can be saved if chamber 5 was in firing position during first shot.
Conclusion :
If second shot is different than first shot only then you can predict the behaviour of third shot.
Moral :
But after all none of this matters because eventually Gabbar would kill all three.